통계 톺아보기/04.군집분석

05_01. 군집분석 S.O.M (self-organizing map)

늉이늉이 2022. 11. 21. 16:35

비지도 학습 중에 비슷한 데이터들을 묶어서 특징을 파악하기 위해 군집분석을 사용하게 되는데요.

그 중에서 S.O.M.의 특징, 장 / 단점 등을 파악해보고자 합니다.

 

1. S.O.M (self-organizing map) 이란?

 

S.O.M은 다양한 변수를 활용하기 때문에 이에 대해 고차원 벡터 공간을 2차원으로 시각화를 하기 위해 제안된 뉴럴 네트워크 기반의 군집분석 모델입니다. 여기서 차원축소와 군집분석이 이용됩니다.

 

Self-organizing map 을 우리 말로 자기 조직화 지도 라고 부르는데요.

그 말은 주어진 입력 패턴에 대하여 정확한 해답을 주지 않고 자기 스스로 학습한다는 것을 의미한답니다.

 

예시를 살펴보겠습니다.

 

아래 그림은 (5,5) 크기 격자이며, 파란색은 고차원 데이터 공간에서의 밀도를 의미하며, 하얀색 점은 현재 학습 데이터의 한 포인트를 의미합니다. 격자 점 중 현재의 포인트와 가장 가까운 점과 그 주변 점들이 학습 데이터에 점점 가까워지면서 세번째 그림처럼 격자가 데이터 공간을 학습하게 되는 것입니다.

 

(출처) 위키피디아

 

 

 

2. 장점

  • 역전파 알고리즘을 이용하는 인공신경망과 달리 하나의 전방 패스(feed-forward flow) 사용하여 속도가 빠름
    • feed-forward flow : 모든 계산이 왼쪽에서 오른쪽으로 진행됨
  • 고차원의 데이터를 저차원의 지도 형태로 형상화하기 때문에 시각적으로 이해가 쉬움
  • 차원 축소 + 군집화 동시 수행 기법
  • 입력 변수의 위치 관계를 그대로 보존하기 때문에 실제 데이터가 유사하면 지도상에도 가깝게 표현됨 → 패턴 발견, 이미지 분석에서 뛰어난 성능 보임
  • 고객 세분화 프로필을 개발하는 직관적인 방법 중 하나
  • 데이터 과학자가 아닌 사람들에게 결과를 설명하기 쉬운 비교적 간단한 알고리즘

 

 

3. 단점

  • SOM 모델의 수학 연산상 복잡성으로 인해 수 천개 이상 데이터 세트 분석 불가능
  • 어떤 유사성/거리 함수를 사용하느냐에 따라 클러스터 내용이 크게 달라질 수 있음
  • 범주형 데이터로는 잘 수행되지 않음

 

 

4. 용어 정리 및 알고리즘

특징, 장/단점을 살펴보았습니다.

그럼 이제 알고리즘을 본격적으로 알아보도록 하겠는데요.

그 전에 과정들을 이해하기 위해 용어들을 간단하게 이해하고 넘어가 보겠습니다.

 

  • 입력층 (input layer) : 입력 벡터를 받는 층으로 입력변수의 개수와 동일한 뉴런수 존재
  • 경쟁층 (competitive layer) : 입력 벡터의 특성에 따라 입력 벡터가 한 점으로 클러스터링 되는 층. SOM은 경쟁 학습으로 각각의 뉴런이 입력 벡터와 얼마나 가까운가를 계산하여 연결강도를 반복적으로 재조정하여 학습
  • 가중치 (weight) : 인공신경망에서 가중치는 각 입력값에 대한 입력값의 중요도를 의미함
  • 노드 (node) : 경쟁층에서 입력 벡터들이 서로의 유사성에 의해 모이는 하나의 영역
  • BMU(Best Matching Unit) : 데이터 포인트와 제일 가까운 노드

 

해당 용어를 이해해서 알고리즘을 이해하기 앞서 아래 그림을 살펴보면 어떻게 노드들이 형성되는지 직관적으로 이해가 되실 것 같습니다.

 

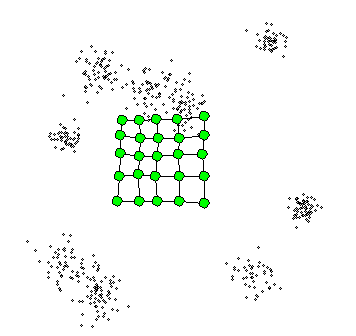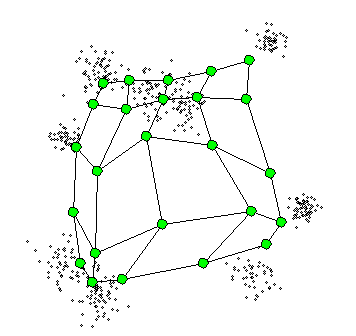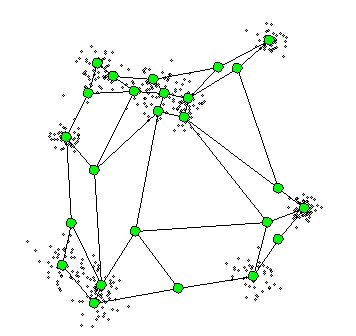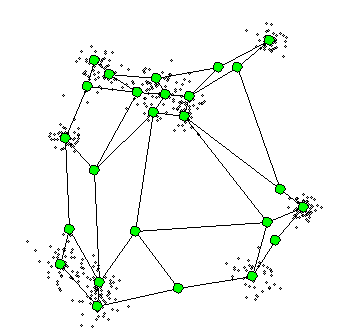
출처 : https://ratsgo.github.io/machine%20learning/2017/05/01/SOM/

 

단계별로 알고리즘 실행 과정을 살펴보도록 하겠습니다. 

  1. 가중치 행렬 각 원소의 값을 임의의 0과 1사이 값으로 초기화
  2. 입력 벡터와 경쟁층에 존재하는 j개 노드에 대해 입력 벡터와 노드 간 거리 Dij 계산
  3. 입력 벡터와 Dij값이 가장 작은 경쟁층 노드 선택 (BMU), 승자 독점 학습 규칙에 따라 위상학적 이웃에 대한 연결 강도 조정
  4. 해당 노드의 가중치(BMU)와 이웃 노드의 가중치 수정
  5. 현재 입력 벡터가 마지막 입력 벡터면 다음 과정으로 이동 아니면 2로 돌아감
  6. 반복 횟수가 최대 반복 횟수면 종료, 아니면 2로 돌아가서 반복

 

 

 

5. Sample Code

from minisom import MiniSom
 
# x, y : the dimension of our SOM map (grid size)
# input_len : feature size
# sigma : sigma is the radius of a different neighborhood in the grid
# learning_rate : the size of how much weight is updated
som = MiniSom(x = x1 , y= y1, input_len = len_x , sigma=0.5, learning_rate=0.5)
# init the weight
som.random_weights_init(X)
# train the model
som.train_random(data = X, num_iteration =100)